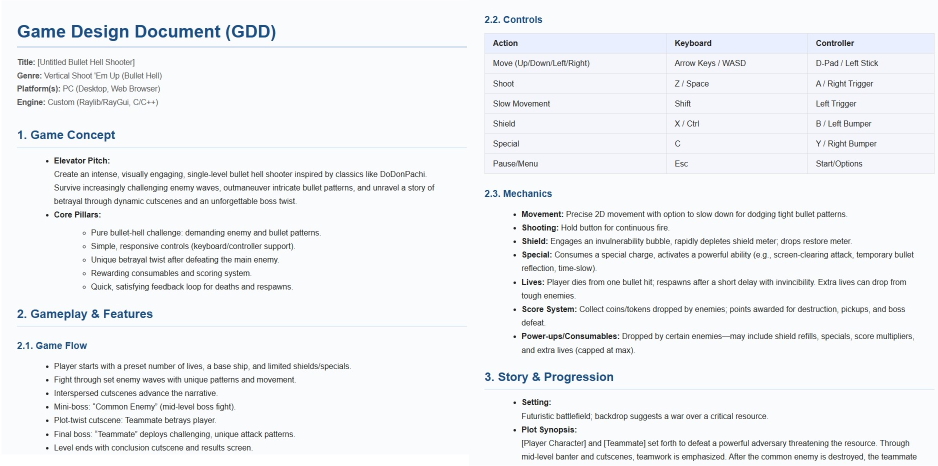
FIXED TIME-STEP GAME LOOP
Jul 30, 2025
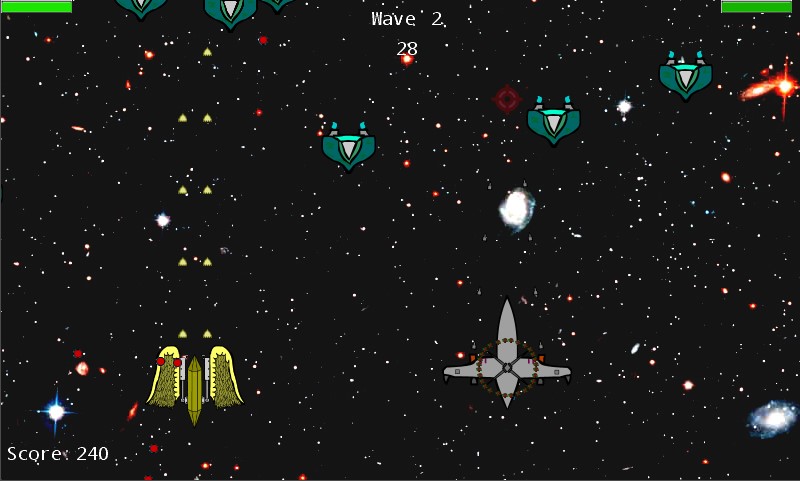
For the majority of simple games I've made, using delta-time in the update function was enough. The games had relatively fixed frame-rates and if there were collision boxes, they were big enough to survive delta-time jumps. However, for the schmup I'm making, I decided it would be best to go with a fixed time-step loop. My reasoning was that, due to the nature of a schmup; high-speed, high-precision, and small hit-boxes, it's critical for near-pixel-perfect simulation.
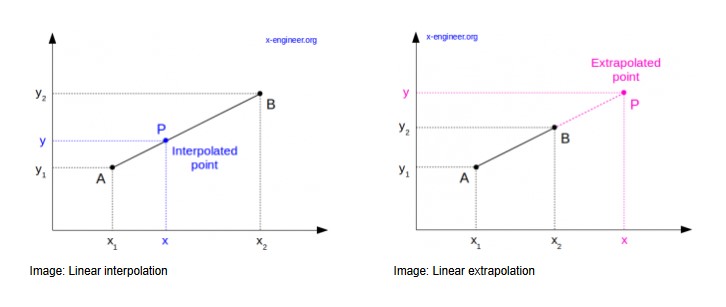
With fixed time-steps and a little bit of math, I can guarantee that hit-boxes won't be missed on variable frame-rates. Additionally, by using interpolation, I can also guarantee that what the player sees is as close to the actual game state as possible. I can't stress enough how important this is for a schmup. Bullets will be flying at high-speed towards hit-boxes only a few pixels wide. If the player is getting hit without seeing a hit, or vise versa, it could completely ruin the gaming experience. The simulation needs to be predictable and the visuals need to match as closely as possible.
double accumulator = 0.0; double prevTimeSec = GetTime(); while (!WindowShouldClose()) { double currTimeSec = GetTime(); double frameTimeSec = currTimeSec - prevTimeSec; // Avoid spiral of death. if (frameTimeSec > 0.25) frameTimeSec = 0.25; prevTimeSec = currTimeSec; accumulator += frameTimeSec; Input(); // Fixed update loop intervals. int loops = 0; while (accumulator >= SKIP_TICKS && loops < MAX_FRAMESKIP) { Update(SKIP_TICKS); accumulator -= SKIP_TICKS; loops++; } double alpha = (double)(accumulator / SKIP_TICKS); Interpolate(alpha); Draw(); }
As you can see in this code example, the flow of logic for each individual frame is as follows:
- Calculate the elapsed time between the start of last frame and the start of this frame.
- If the elapsed time is greater than 0.25 seconds, set it to 0.25 to avoid The Spiral of Death.
- Increment our accumulator by the elapsed time.
- Run the update function with a fixed delta-time, subtracting it from the accumulator, until we either run out of elapsed time or hit a maximum threshold.
- Calculate the interpolation factor (the fraction of time that has passed since the last logic update, divided by the fixed update interval).
- Execute the interpolation function to produce and intermediary "draw state".
- Draw the frame based on the interpolated draw state.
For now this works perfectly and I can adjust both the frame-rate and update-rate independently. I am slightly concerned though at the added complexity due to interpolation. Because of this, I have to keep track of a separate state, the "draw state". This way, when there's not enough time to run another update loop, I can still draw the frame where objects would be if it did update. This keeps the visuals smooth while making the simulation (update calculations) more reliable with fixed steps.
Here is an example data structure used to test the game loop:
struct Device { Vector2 prevPos; Vector2 currPos; // Normally all you need is this. Vector2 rendPos; };
This structure tracks the location of a ball moving across the screen. Normally, without interpolation, you just have one position which is incremented by delta-time or fixed-step during the update. However, with the addition of interpolation, I now have to track both the previous position and the render position. That function looks like this:
void Interpolate(double alpha) { device.rendPos.x = device.prevPos.x + (device.currPos.x - device.prevPos.x) * alpha; device.rendPos.y = device.prevPos.y + (device.currPos.y - device.prevPos.y) * alpha; }
In conclusion, I'm glad I have my game loop implemented, since it is the backbone of my game. However, I will be reevaluating it in the future after I have added more systems that will prove the viability of this strategy.